AMPLIFICATEURS OPÉRATIONNELS

AMPLIFICATEURS OPÉRATIONNELS

Macrocomposant électronique à faible coût, l’amplificateur opérationnel a été conçu, dès l’origine, pour réaliser, en association avec quelques composants, des opérations sur des signaux analogiques, en basse fréquence et faible puissance.

1. Opérateurs

Notions générales

Les systèmes électroniques réalisent le traitement et la transmission de signaux électriques porteurs d’informations dans un but de connaissance ou de commande. Ce traitement est une succession d’opérations élémentaires mathématiquement ou technologiquement. Le système est donc constitué par une association de sous-ensembles ou de modules diversifiés, appelés opérateurs. Les opérateurs linéaires sont régis par un système d’équations différentielles à coefficients constants; l’opérateur «multiplication par une constante» est appelé usuellement, et parfois à tort, amplificateur; le sommateur réalise l’addition pondérée; le soustracteur non pondéré est un amplificateur différentiel; l’intégrateur est un filtre particulier. Parmi les opérateurs non linéaires , citons le comparateur de signes, dont la sortie ne prend que deux états, les redresseurs mono- et bi-alternance, les comparateurs à hystérésis, le limiteur. Les convertisseurs analogique/numérique, amplituderéquence, l’échantillonneur sont des opérateurs technologiquement élémentaires, puisqu’ils existent tous en circuits intégrés.

Les signaux et donc les opérateurs sont appelés analogiques si l’amplitude de la grandeur porteuse de l’information peut prendre toute valeur dans un intervalle donné; au contraire, si le nombre d’états est fini (deux en général), les signaux sont dits numériques.

Les opérateurs ont un sens d’action privilégié. Ils possèdent une (des) entrée(s) e et une sortie s telle que s = f (e ); l’application d’un signal en s ne donne pas en e une valeur e = f ^-1(s ); l’opération inverse ne peut se réaliser ainsi. Un opérateur «valable» est, par essence, unidirectionnel.

L’information appliquée à l’entrée de l’opérateur provient d’un autre opérateur ou d’un capteur, qui est appelé source ; l’information traitée est délivrée à un système qui est appelé charge . Ainsi, dans une chaîne d’opérateurs, chacun d’eux joue le rôle de source pour le suivant et de charge pour le précédent.

Opérateurs électroniques

Les systèmes électroniques traitent des grandeurs électriques. Ce sont des tensions ou des courants ; le cas d’impédances s’y ramène par l’adjonction d’une source fixe dite de polarisation. L’application d’une tension ou la circulation d’un courant impose l’accès à l’«entrée» par deux bornes; il en est de même en «sortie».

Le paramètre de la grandeur (tension ou courant) porteur de l’information peut être l’amplitude instantanée ou la durée de l’impulsion... ou la fréquence ou la phase dans le cas d’un signal périodique.

Amplificateur ou source commandée

Caractérisons l’opérateur électronique réalisant la multiplication par une constante; il a la structure d’un quadripôle à deux bornes d’entrée et deux bornes de sortie; la source associée est un dipôle; il en est de même de la charge. Compte tenu de la diversité possible de grandeurs utiles d’entrée et de sortie (tension ou courant), on rencontre quatre types d’opérateurs notés SCVV, SCVI, SCIV, SCII. L’opérateur SCVI, par exemple, est appelé «source commandée (ou liée) tension donne courant» et sa relation caractéristique liant le signal utile de sortie à celui d’entrée est i ^s = Kv^e . Noter que le coefficient K est ou non sans dimension; dans l’exemple cité, il est homogène à une admittance, c’est pourquoi cet opérateur SCVI est parfois appelé amplificateur à transadmittance. De même, l’opérateur SCIV est un amplificateur à transimpédance; l’opérateur SCVV est un amplificateur de tension; l’opérateur SCII est un amplificateur de courant.

La source qui délivre la grandeur utile (tension ou courant) est modélisable par sa représentation de Thévenin (force électromotrice e ^e en série avec une résistance, dite de source, R^g ) ou par sa représentation de Norton (courant électromoteur j ^e en parallèle sur une résistance interne R^g ). Le cas d’une impédance de source Z^g est une généralisation de R^g . L’information est supposée portée par e ^e ou j ^e . Les schémas équivalents sont donnés sur la figure 1.

Vis-à-vis de sa charge, l’opérateur se comporte comme une source; il est modélisable par Thévenin ou Norton, donc par une source de f.é.m. e ^s ou de c.é.m. j ^s , de résistance, dite de sortie, R^s .

La fonction même de multiplication par une constante impose à e ^s ou j ^s d’être proportionnel au courant i ^e (ou à la tension v^e ) appliqué à l’entrée de l’opérateur. Afin d’obtenir l’égalité e ^s = Ke ^e (ou i ^s = Ke ^e ou e ^s = Kj ^e ...), il faut que v^e soit égal à e ^e ou i ^e à j ^e : le prélèvement du signal e ^e ou j ^e et son application à l’opérateur doivent s’effectuer sans perte dans la résistance R^g . L’entrée de l’opérateur SCVI ou SCVV doit donc être équivalente à un circuit ouvert (on dit que la résistance d’entrée R^e est infinie), celle de l’opérateur SCIV ou SCII doit être un court-circuit (R^e est nulle). Cela est modélisé sur les schémas de la figure 1. D’autre part, pour que la tension utile v^s (ou le courant utile j ^s ) en sortie de l’opérateur soit indépendant de la charge (supposée par simplification être une résistance R^u ), il faut que la résistance de sortie R^s de l’opérateur soit sans influence: R^s doit être nulle pour les opérateurs SCVV ou SCIV, infinie dans les deux autres cas. La figure 1 donne aussi les modèles des opérateurs SCVV et SCII; les deux autres cas s’en déduisent.

Les opérateurs correspondant à ces modèles sont idéaux ; l’opérateur réel doit s’en approcher pour être «valable». Les imperfections proviennent du paramètre K lui-même, car sa valeur fluctue avec les conditions de fonctionnement et en particulier avec la fréquence du signal de commande (notion de bande passante). D’autres imperfections sont dues aux valeurs non idéales des résistances R^e et R^s , car celles-ci créent des effets de consommation et de division de tension ou de courant en entrée et en sortie. Signalons l’existence possible d’un décalage interne défini par s (e = 0) non nul.

Un amplificateur performant peut délivrer une puissance (v^s i ^s ) à la charge, alors même que la source n’en fournit pas ou très peu (v^e i ^e 年 0). Cela implique l’existence d’un apport d’énergie interne à l’opérateur, généralement réalisé à partir du secteur ou par piles. Cependant, cet apport d’énergie est limité et, par conséquent, la puissance délivrée à la charge l’est aussi: un amplificateur présente des phénomènes non linéaires de saturation en tension ou en courant de sortie ainsi qu’en vitesse d’évolution (appelée vitesse de balayage).

On sait construire communément un amplificateur à l’aide de transistors, et la réalisation en circuit intégré abaisse considérablement les coûts. Toutefois, les structures simples ont un gain K peu fiable, c’est-à-dire que sa valeur est très dépendante de celle des coefficients 廓 des transistors constitutifs; or, d’une part, 廓 peut varier dans un rapport dix d’un échantillon à l’autre, d’autre part, cette valeur dérive avec la température et le temps. Pour cette raison, on utilise systématiquement des structures à rétroaction qui, nous allons le voir, stabilisent la valeur du coefficient.

2. Rétroaction

Le champ d’applications du concept de rétroaction (ou réaction) déborde largement le domaine de l’électronique. Une structure à réaction associe deux opérateurs et un soustracteur, appelé parfois à tort comparation, selon le schéma-bloc de la figure 2.

Pour simplifier, considérons le cas où les deux opérateurs sont du type «multiplication par une constante». On peut alors écrire: s = 猪e , e ⁰ = 廓s , 﨎 = e 漣 e ⁰, donc s /e = H = 猪/(1 + 猪廓). Le rapport H est appelé «gain en boucle fermée».

En électronique, ces systèmes à rétroaction trouvent leur principal intérêt dans le cas particulier où 猪廓 est très supérieur à l’unité car, alors, H vaut pratiquement 1/ 廓: le système bouclé réalise l’opération inverse à celle de l’opérateur 廓 si l’opérateur 猪 a un gain «très grand».

La rétroaction permet d’atténuer l’effet des fluctuations de 猪, puisque H en est quasi indépendant tant que 猪 est de valeur élevée.

La rétroaction atténue les imperfections de l’opérateur 猪, dit de chaîne directe: l’existence d’un décalage s ( 﨎 = 0) = s ⁰ non nul, interne à l’opérateur 猪, entraîne celle d’un décalage s (e = 0) pour le système bouclé, mais de valeur atténuée puisque s (e = 0) = s ⁰/(1 + 猪⁰ 廓).

La rétroaction peut poser des problèmes de stabilité . Les coefficients 猪 et 廓 de tout système physique ne peuvent être des grandeurs purement réelles. Pour simplifier, supposons 廓 réel et l’opérateur 猪 régi par une équation différentielle de premier ordre: s + (1/ 諸⁰) ds /dt = 猪⁰ 﨎, où 猪⁰ et 諸⁰ sont réels. Calculons la réponse s (t ) du système à une variation e (t ) en échelon (e (t ) = 0 si t 麗 0; e (t ) = E constant si t 礪 0). On obtient:

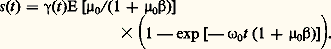La lecture de cette relation montre que s (t ) atteint sa position d’équilibre selon une loi exponentielle à condition que 1 + 猪⁰ 廓 soit positif. La réponse est divergente dans l’hypothèse inverse. En pratique, et lorsque 猪⁰ est très supérieur à l’unité, le système est stable si 廓 est positif, il est instable si 廓 est négatif. Il faut remarquer qu’une permutation des entrées e et e ⁰ revient à un changement de signe pour 廓; le système stable est rendu instable.

Les équations différentielles régissant tous les systèmes physiques sont d’un ordre supérieur à l’unité, et cela explique pourquoi la réponse s (t ) à un échelon peut présenter des phénomènes d’oscillations transitoires.

La rétroaction possède d’autres propriétés dont la plus classique est que le produit gain 憐 bande passante d’un système bouclé du premier ordre est constant. Cela se démontre pour le système pris en exemple:

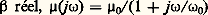puisque:

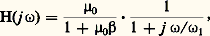où 諸¹ = 諸⁰(1 + 猪⁰ 廓); la valeur du gain dans la bande passante est H⁰ = 猪⁰/(1 + 猪⁰ 廓) et la pulsation de coupure est 諸¹; on vérifie que H⁰ 諸¹ vaut 猪⁰ 諸⁰ quelle que soit la valeur de 廓, donc du gain H⁰.

La théorie de la rétroaction s’applique en électronique en particulier aux sources commandées de grand gain 猪, associées à un soustracteur et à un réseau de réaction 廓 constitué d’impédances; les valeurs de ces impédances déterminent seules le gain du système dans la bande passante.

3. Amplificateur différentiel

Un amplificateur différentiel associe les opérations de soustraction et de multiplication par une constante. Dans le cas usuel où les signaux sont des tensions toutes prises par rapport à une même référence, appelée masse, le modèle idéal est celui de la figure 3, où on a explicité la relation caractéristique définissant le gain différentiel 猪: v^s = 猪(e ⁺ 漣 e ^-) = 猪﨎.

Les amplificateurs de tension différentiels réels présentent des défauts, extrapolés de ceux de l’opérateur SCVV énumérés auparavant; le modèle prenant en compte les imperfections linéaires est donné dans la figure 4. On y note l’existence d’impédances de sortie Z⁰, d’entrées de mode commun Z^{c +}, Z^{c -} et de mode différentiel Z^d , de courants de polarisation i ^{b +} et i ^{b -}, d’une tension de décalage ramenée à l’entrée v^d et d’un facteur de rejection de mode commun noté F^r . Les courants de polarisation sont les courants base ou grille des transistors d’entrée du circuit, la tension v^d provient d’une symétrie imparfaite de la structure interne et le décalage en sortie de l’opérateur v^s (e ⁺ = e ^- = 0) vaut 猪(v^d 漣 R^{g +}i ^{b +} + R^{g -}i ^{b -}); le facteur de rejection F^r traduit l’existence d’un gain non nul, dit de mode commun et défini par :

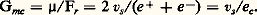L’amplificateur différentiel réel possède, comme l’opérateur SCVV, des limitations non linéaires: saturation de tension, de courant et vitesse de balayage.

4. Amplificateur opérationnel

Caractérisation

Par conception, l’amplificateur opérationnel est un amplificateur de tension différentiel de très grand gain. Le modèle, à source liée, de l’amplificateur opérationnel dit idéal est donc celui de la figure 3, avec 猪 tendant vers l’infini. Le modèle de l’amplificateur opérationnel réel, en régime linéaire, est celui de la figure 4.

Le symbole est celui de la figure 5, où on note l’existence de bornes d’accès pour les sources/apport d’énergie, bornes distinctes des bornes d’accès des signaux utiles. Une seule source d’alimentation est parfois suffisante, mais les signaux ne peuvent, alors, prendre des valeurs négatives et positives (cas des signaux alternatifs et en particulier sinusoïdaux). Sur la figure 5, on remarque que la circulation des courants entre réseaux utiles et sources d’alimentation s’effectue grâce à l’existence d’un nœud commun à tous les réseaux, appelé masse.

Les fabricants d’amplificateurs opérationnels fournissent des feuilles de spécifications donnant, pour chaque produit, les limites de fonctionnement à ne pas dépasser sous peine de destruction et les valeurs typiques ou garanties des paramètres du modèle de la figure 4. On doit savoir que, pour un prix modique, on peut acheter un amplificateur opérationnel d’encombrement boîtier de 10 mm 憐 6 mm 憐 3 mm, à alimenter en 梁 15 V, permettant de traiter des tensions de valeurs comprises entre + 10 et 漣 10 V, pouvant délivrer 梁 5 mA et 梁 10 V à la charge et dont les impédances d’entrée atteignent 10¹⁰ 行; |v^d | est inférieur à 5 mV, i ^b à 10^-10A; le gain 猪 dépasse 5. 10⁴ et la vitesse de balayage vaut 10 V/ 猪s.

Le rapport qualité/prix et la miniaturisation sont spectaculaires; ils ont pu être atteints grâce à l’évolution technologique rapide qui a eu lieu entre 1960 et 1975 en microélectronique, tant dans le domaine des circuits logiques que dans celui des modules analogiques. La figure 6 a donne une vue d’un circuit intégré réalisant un amplificateur opérationnel classique; sa surface est de 2 mm²; le schéma interne à transistors correspondant est donné par la figure 6 b.

Réalisation de sources commandées

L’amplificateur opérationnel trouve sa justification et son plein emploi dans les structures à rétroaction.

La transposition du schéma-bloc de la figure 2 aux opérateurs électroniques associant l’amplificateur opérationnel en chaîne directe ( 猪) et une ou deux résistances en chaîne de retour ( 廓) conduit à quatre configurations; seuls les opérateurs SCIV et SCVV présentent une charge référencée à la masse commune; leur structure est donnée par la figure 7.

L’analyse directe de l’opérateur SCVV peut se conduire selon le raisonnement maintenant présenté. Supposons l’amplificateur opérationnel non à saturation en tension, courant ou vitesse, donc en régime linéaire, alors la relation v^s = 猪﨎 est vérifiée. Supposons l’amplificateur opérationnel idéal , donc tel que 猪 soit infini et sans imperfection. La tension de sortie étant de valeur finie, 﨎 doit être nul. Les courants i ⁺ et i ^- sont donc nuls. Ainsi la f.é.m. e se retrouve aux bornes de la résistance R; l’amplificateur opérationnel délivre un courant i ⁰ à R et R tel que e = Ri ⁰; la tension v^s aux bornes de la charge R^u est la même qu’aux bornes de (R + R ):

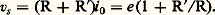Le courant i ⁺ étant nul, l’impédance d’entrée de l’opérateur réalisé est infinie et R^g est sans influence; la valeur de la charge R^u n’apparaissant pas dans l’expression v^s = Ke , l’impédance de sortie est nulle; l’opérateur réalisé est bien un amplificateur de tension SCVV, de gain K égal à (1 + R /R); cet opérateur SCVV serait idéal si l’amplificateur opérationnel l’était.

La justification des positions respectives des entrées inverseuse (face=F0019 漣) et non inverseuse (+) s’effectue par l’étude de la stabilité de ce système bouclé selon la méthode exposée au chapitre Rétroaction .

Il est essentiel de noter que l’amplificateur opérationnel idéal inclus dans un système bouclé et fonctionnant en régime linéaire présente une tension différentielle 﨎 et des courants d’entrée nuls, une tension et un courant de sortie «libres», c’est-à-dire dont les valeurs sont strictement imposées de l’extérieur (ici v^s = e (1 + R /R) et i ^s = e (R + R + R^u )/RR^u ).

L’examen du fonctionnement de l’opérateur SCIV confirme les résultats précédents dans les mêmes hypothèses: si l’amplificateur opérationnel est idéal et en régime linéaire, 﨎 est nul, R^g est sans influence, i ^- est nul et j circule dans R , ainsi v^s vaut 漣 R j , qui est indépendant de R^u . Noter que le courant i ^u = v^s /R^u circulant dans R^u est de signe opposé à j ; c’est la sortie de l’amplificateur opérationnel qui fournit ou absorbe la somme des courants de source (j ) et de charge (i ^u ).

Influence des imperfections

L’analyse de l’influence des imperfections linéaires de l’amplificateur opérationnel, modélisées pour mémoire dans la figure 4, sur les performances d’une source commandée s’effectue simplement pas à pas en considérant chaque imperfection l’une indépendamment des autres et en calculant la variation de la tension de sortie correspondante. On montrerait ainsi, en particulier, que:

pour l’opérateur SCIV.

Du calcul systématique de toutes ces expressions, on peut déduire un choix optimal du type d’amplificateur opérationnel et des valeurs des composants associés à utiliser pour la réalisation pratique répondant à un cahier des charges déterminé.

Exemples d’autres opérateurs linéaires

En pratique, les signaux utiles d’un système sont généralement des tensions toutes prises par rapport à une référence commune. La figure 8 propose quelques opérateurs issus des configurations de base de la figure 7.

Le suiveur est issu de l’opérateur SCVV de base avec R nulle et R infinie; son gain est unitaire; il est utilisé comme «isolateur» vis-à-vis des valeurs d’impédances de source et de charge.

Le sommateur/inverseur est issu de l’opérateur SCIV de base (v^s = 漣 R j ); le courant j est réalisé par la sommation des courants i ⁿ ; chaque courant i ⁿ injecté est obtenu à partir de la tension ve ⁿ de source par la résistance Rⁿ de conversion tension/courant; i ⁿ vaut ve ⁿ /Rⁿ , car v^- est nul en régime linéaire et pour un amplificateur opérationnel idéal. Ainsi:

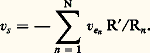Les résistances de source R^gn interviennent dans la relation liant v^s à la f.é.m. e ⁿ de la source, puisque i ⁿ = e ⁿ /(Rⁿ + R^gn ). On pourrait s’en affranchir par l’emploi d’un suiveur intercalé entre la source et Rⁿ sur chaque voie.

L’inverseur de tension constitue un cas particulier du sommateur précédent, une seule source est appliquée et la relation v^s = 漣 e R /(R + R^g ) justifie l’appellation d’amplificateur inverseur de tension.

Des filtres peuvent être obtenus par extrapolation de la configuration «inverseur» au cas d’impédances associées non purement résistives. En pratique, les dipôles Z et Z sont des associations de type (R, C) série ou parallèle; on réalise ainsi des filtres élémentaires de type passe-bas, passe-haut, coupe-bande ou passe-bande. Des filtres plus élaborés nécessitent l’emploi de plusieurs amplificateurs opérationnels; en particulier, il existe un circuit intégré à quatre amplificateurs opérationnels réalisant un filtre du second ordre, dit universel car on peut imposer la valeur de ses paramètres caractéristiques à l’aide de quelques résistances externes seulement.

L’intégrateur est un cas particulier de filtre: Z est une résistance et Z un condensateur; la relation entrée-sortie est:

L’opérateur réalise bien l’intégration en fonction du temps; on peut appliquer la condition initiale v^{s 0} par charge antérieure du condensateur. L’existence du courant de polarisation i ^{b -} conduit à l’existence d’une tension de sortie parasite de valeur v^s (e = 0, i ^b ) = i ^{b -}t /C; cette tension dérive ainsi continuement avec le temps. Ce phénomène interdit l’emploi de cet opérateur hors le cas d’un ensemble bouclé qui autocompense cette dérive.

Le soustracteur peut être regardé comme l’association de l’opérateur SCVV de base et de l’inverseur. La relation caractéristique est: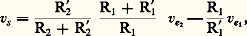

soit v^s = a ²ve ² 漣 a ¹ve ¹. Ce circuit est différentiel si les coefficients a ² et a ¹ sont égaux; cette condition est impossible à réaliser en toute rigueur, compte tenu de la tolérance (au moins 0,1 p. 100) des résistances. C’est pourquoi cette structure est souvent insatisfaisante; les circuits intégrés qui réalisent un amplificateur différentiel de bonnes performances ont une structure très symétrique; leur gain différentiel est ajustable par le biais d’une unique résistance externe, mais le prix est environ vingt fois celui d’un amplificateur opérationnel.

Exemples d’opérateurs non linéaires

On a énuméré au chapitre Opérateurs quelques-uns des opérateurs non linéaires usuels. Leur réalisation suppose l’emploi de composants électroniques non linéaires (diodes par exemple) associés à l’amplificateur opérationnel ou l’exploitation de propriétés non linéaires de l’amplificateur opérationnel lui-même. La figure 9 propose deux exemples.

Le comparateur est réalisé directement par un seul amplificateur opérationnel non inclus dans une boucle. Si e est supérieur à une tension de référence E, 﨎 est positif; puisque le gain 猪 de l’amplificateur opérationnel est élevé, la tension de sortie v^s ne peut respecter la relation linéaire v^s = 猪﨎 et la sortie est à saturation de tension. La valeur de cette tension est imposée par celles des sources d’alimentation V⁺ et V^-; en première approche v^s ( 﨎 礪 0) = V⁺. De même, si e est inférieur à E, 﨎 est négatif et v^s ( 﨎 麗 0) = V^-. Cela n’est vrai que si les valeurs de e et E sont incluses dans l’intervalle [V^-, V⁺] sous peine de destruction. Cet opérateur est bien un comparateur d’amplitudes: e 麗 E, v^s = V^-; e 礪 E, v^s = V⁺.

Le redresseur associe un amplificateur opérationnel et une diode. Si la diode est conductrice, elle a pour modèle un court-circuit et on reconnaît dans le schéma le suiveur de la figure 8: v^s = e . L’hypothèse «diode conductrice» est équivalente à un courant i positif; i ^- étant nul, v^s vaut R^u i ; la relation v^s = e implique donc la condition e positif. Si la diode est bloquée, c’est un interrupteur ouvert, i est nul, v^s est nul mais la sortie de l’amplificateur opérationnel (non bouclé) est à saturation positive V⁺ ou négative V^-. La condition «diode bloquée» est équivalente à v négatif, donc à V^-; cela implique que 﨎 donc e soient négatifs. On vérifie ainsi que le circuit laisse passer les alternances positives et rejette les alternances négatives du signal d’entrée. Ce circuit donne de meilleurs résultats qu’une simple diode dans le domaine d’emploi de l’amplificateur opérationnel (face=F0019 梁 10 V, 梁 5 mA), car il élimine l’influence de la tension de déchet (0,6 V) de la diode conductrice, en application des propriétés des systèmes bouclés vis-à-vis du décalage interne. Ce circuit est la base d’opérateurs divers tels le limiteur ou le module le plus grand de deux.

5. Exemples de systèmes et domaines d’application

Les calculateurs analogiques effectuaient la résolution d’un système d’équations différentielles, linéaires ou non, en temps réel. Ils existaient antérieurement aux ordinateurs, puisqu’ils étaient employés durant la Seconde Guerre mondiale comme calculateurs de tir. Ils ont survécu jusqu’en 1970-1975 pour leur aptitude à la résolution en temps réel , que seuls les ordinateurs récents sont capables d’effectuer. Ils se présentaient sous forme modulaire et associaient aux opérateurs linéaires (sommateur, inverseur, intégrateur) des opérateurs non linéaires (comparateur, redresseur, multiplieur); l’expérimentateur câblait à la demande les interconnexions entre modules, il choisissait les valeurs des coefficients caractéristiques par un jeu de potentiomètres. Ces calculateurs étaient, en ce sens, universels et souples d’emploi. Ils ont donné naissance, d’une part, aux calculateurs hybrides associant ordinateur et modules analogiques, d’autre part aux simulateurs précâblés et spécialisés. Ils étaient souvent, et à tort, considérés davantage comme calculateurs mathématiques que comme systèmes de traitement de signaux physiques porteurs d’information.

À l’opposé, la compréhension du fonctionnement du multivibrateur astable classique donné dans la figure 10 est clarifiée si la structure est reconstruite sous la forme d’un système associant un ensemble d’opérateurs en chaîne bouclée. Par identification, on peut reconnaître dans le diviseur (R, C) une médiocre réalisation d’un intégrateur et dans l’amplificateur opérationnel un comparateur de tension (donc l’association d’un soustracteur et d’un comparateur de signe) attaqué par la sortie s ¹ de l’intégrateur et par une fraction 廓 du signal de sortie. On a ainsi les relations:

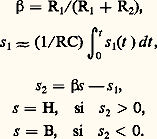Leur analyse, pas à pas, donne les caractéristiques du signal carré délivré en sortie: niveaux H = V⁺, B = V^-; période T = 2 RC Log (1 + 2 R¹/R²). On peut remarquer que l’ensemble bouclé soustracteur, comparateur de signes (donc l’amplificateur opérationnel associé à R¹ et R²) est un comparateur à hystérésis ou trigger de Schmitt. Il faut savoir que l’emploi d’un véritable intégrateur à amplificateur opérationnel en remplacement du diviseur (R, C) permet d’obtenir en s ¹ des signaux triangulaires vrais.

Les deux exemples cités (calculateur universel et structure électronique compacte) sont des cas d’applications extrêmes. À l’heure actuelle et puisque l’amplificateur opérationnel est de faible coût, on a de plus en plus tendance à concevoir les systèmes de traitement par transposition directe d’un schéma synoptique. La description des diverses opérations à réaliser est transposée en un assemblage de circuits intégrés réalisant pour chacun d’eux (ou en association avec quelques composants (R, C) ou diodes) une fonction élémentaire, bien déterminée et de caractéristiques facilement maîtrisables ou ajustables.

Les domaines d’emploi de l’amplificateur opérationnel tendent à s’élargir au fur et à mesure de l’amélioration de ses caractéristiques; on le rencontre, par exemple, dans les chaînes de régulation, dans la commande de processus, dans les étages basse puissance en électronique industrielle, dans certains produits «grand public» et en instrumentation basse fréquence. Ils ont considérablement simplifié la tâche des concepteurs: l’association de modules types de bonnes performances, de faible coût et à spécifications ajustables, a remplacé l’emploi de structures «imbriquées», «compactes», peu fiables, difficilement analysables et dépannables.

Encyclopédie Universelle. 2012.